It'll have some potassium in it.
- .
- daniel sharman dating!
- profile text dating site!
- .
- dating kelly axe!
- who is jennifer lawrence dating june 2013!
- free dating website in pune!
I'm maybe over doing it. It's a very scarce isotope. But it'll have some potassium in it. And it might already have some argon in it just like that. But argon is a noble gas. It's not going to bond anything. And while this lava is in a liquid state it's going to be able to bubble out.
It'll just float to the top. It has no bonds. And it'll just evaporate. I shouldn't say evaporate. It'll just bubble out essentially, because it's not bonded to anything, and it'll sort of just seep out while we are in a liquid state. And what's really interesting about that is that when you have these volcanic eruptions, and because this argon is seeping out, by the time this lava has hardened into volcanic rock-- and I'll do that volcanic rock in a different color.
- Navigation menu.
- K-Ar dating calculation (video) | Khan Academy.
- dating ariane bar trivia answers!
- work of art miles and nicole dating!
By the time it has hardened into volcanic rock all of the argon will be gone. It won't be there anymore. And so what's neat is, this volcanic event, the fact that this rock has become liquid, it kind of resets the amount of argon there. So then you're only going to be left with potassium here. And that's why the argon is more interesting, because the calcium won't necessarily have seeped out.
And there might have already been calcium here. So it won't necessarily seep out. But the argon will seep out. So it kind of resets it.
K-Ar dating calculation
The volcanic event resets the amount of argon So right when the event happened, you shouldn't have any argon right when that lava actually becomes solid. And so if you fast forward to some future date, and if you look at the sample-- let me copy and paste it. So if you fast forward to some future date, and you see that there is some argon there, in that sample, you know this is a volcanic rock. You know that it was due to some previous volcanic event. You know that this argon is from the decayed potassium And you know that it has decayed since that volcanic event, because if it was there before it would have seeped out.
K–Ar dating - Wikipedia
So the only way that this would have been able to get trapped is, while it was liquid it would seep out, but once it's solid it can get trapped inside the rock. And so you know the only way this argon can exist there is by decay from that potassium So you can look at the ratio. And so for every one of these argon's you know that there must have been 10 original potassium's. And so what you can do is you can look at the ratio of the number of potassium's there are today to the number that there must have been, based on this evidence right over here, to actually date it.
And in the next video I'll actually go through the mathematical calculation to show you that you can actually date it. And the reason this is really useful is, you can look at those ratios. And volcanic eruptions aren't happening every day, but if you start looking over millions and millions of years, on that time scale, they're actually happening reasonably frequent. And so let's dig in the ground. So let's say this is the ground right over here.
And you dig enough and you see a volcanic eruption, you see some volcanic rock right over there, and then you dig even more. There's another layer of volcanic rock right over there. So this is another layer of volcanic rock. So they're all going to have a certain amount of potassium in it. This is going to have some amount of potassium in it. And then let's say this one over here has more argon This one has a little bit less.
And using the math that we're going to do in the next video, let's say you're able to say that this is, using the half-life, and using the ratio of argon that's left, or using the ratio of the potassium left to what you know was there before, you say that this must have solidified million years ago, million years before the present. And you know that this layer right over here solidified. Let's say, you know it solidified about million years before the present.
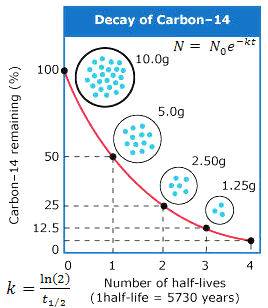
And let's say you feel pretty good that this soil hasn't been dug up and mixed or anything like that. It looks like it's been pretty untouched when you look at these soil samples right over here.
Keep Exploring Britannica
And let's say you see some fossils in here. Then, even though carbon dating is kind of useless, really, when you get beyond 50, years, you see these fossils in between these two periods. It's a pretty good indicator, if you can assume that this soil hasn't been dug around and mixed, that this fossil is between million and million years old.
Then you have these fossils got deposited. These animals died, or they lived and they died. And then you had this other volcanic event. So it allows you, even though you're only directly dating the volcanic rock, it allows you, when you look at the layers, to relatively date things in between those layer. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Science Biology History of life on Earth Radiometric dating. Carbon 14 dating 1.
Carbon 14 dating 2. Atomic number, atomic mass, and isotopes. Video transcript In the last video, we give a bit of an overview of potassium-argon dating. In this video, I want to go through a concrete example. And it'll get a little bit mathy, usually involving a little bit of algebra or a little bit of exponential decay, but to really show you how you can actually figure out the age of some volcanic rock using this technique, using a little bit of mathematics.
So we know that anything that is experiencing radioactive decay, it's experiencing exponential decay. And we know that there's a generalized way to describe that. And we go into more depth and kind of prove it in other Khan Academy videos. But we know that the amount as a function of time-- so if we say N is the amount of a radioactive sample we have at some time-- we know that's equal to the initial amount we have.
We'll call that N sub 0, times e to the negative kt-- where this constant is particular to that thing's half-life. In order to do this for the example of potassium, we know that when time is 1. So let's write it that way.
So let's say we start with N0, whatever that might be. It might be 1 gram, kilogram, 5 grams-- whatever it might be-- whatever we start with, we take e to the negative k times 1. That's the half-life of potassium We know, after that long, that half of the sample will be left. Whatever we started with, we're going to have half left after 1. Divide both sides by N0. And then to solve for k, we can take the natural log of both sides. The natural log is just saying-- to what power do I have to raise e to get e to the negative k times 1. So the natural log of this-- the power they'd have to raise e to to get to e to the negative k times 1.
Or I could write it as negative 1. That's the same thing as 1. We have our negative sign, and we have our k. And then, to solve for k, we can divide both sides by negative 1. And so we get k. And I'll just flip the sides here.
Radiometric dating
And what we can do is we can multiply the negative times the top. Or you could view it as multiplying the numerator and the denominator by a negative so that a negative shows up at the top. And so we could make this as over 1. Let me write it over here in a different color. The negative natural log-- well, I could just write it this way. If I have a natural log of b-- we know from our logarithm properties, this is the same thing as the natural log of b to the a power. And so this is the same thing. Anything to the negative power is just its multiplicative inverse.
So this is just the natural log of 2. So negative natural log of 1 half is just the natural log of 2 over here. So we were able to figure out our k. It's essentially the natural log of 2 over the half-life of the substance. So we could actually generalize this if we were talking about some other radioactive substance. And now let's think about a situation-- now that we've figured out a k-- let's think about a situation where we find in some sample-- so let's say the potassium that we find is 1 milligram.